What’s 5 x 3?
How about 4 x 6?
You might think those are simple questions, but a third grader had points taken off on an exam recently after giving the answers 15 and 24, respectively.
“But those are the right answers,” you say. And a lot of people on Reddit would agree with you.
So what’s going on?

At first glance, the child seems to have done everything right.
After all, if kids are told to use the “repeated addition strategy” to solve 5 x 3, then writing down 5 + 5 + 5 makes as much sense as writing 3 + 3 + 3 + 3 + 3. You’ll get 15 either way. That’s how the commutative property works.
Same with the next question. If kids have to draw an “array” to solve 4 x 6, why would the orientation matter as long as they ultimately got to 24?
There are only two possible conclusions: (1) This teacher is an idiot, or (2) The people complaining don’t know what’s going on here.
Let’s assume for a second that this teacher isn’t an idiot. (I know. I know. Bear with me for a minute.)
What possible explanation could there be for deducting points from this poor child’s exam?
You have to understand that one of the big things math teachers are trying to do these days is get kids prepared for the math classes they may take in the future. So when they’re learning how to add in first grade, they’re also being taught methods that will help them add more complicated numbers a few years down the road.
Take multiplication for a second.
How do you know that 11 x 7 = 77? Maybe you memorized your times tables or maybe you learned the “trick” about multiplying small numbers by 11 (you just have to repeat the number twice).
That’s nice. You’ll get the right answer. But it doesn’t really explain what’s going on with the numbers. After all, if I ask those same kids to solve 11 x 27, they’re going to be stuck.
HOWEVER.
What if we taught kids to think about 11 x 7 a different way, right up front? Instead of focusing on memorization or quick tricks, what if we told them to break down the problem a different way? What if we taught them to do 10 x 7 (which is easy enough for anyone) and then add another 7 to it?
I know that seems slightly more complicated than before, but here’s the beauty of it: It won’t be long before they can do 11 x 27 in their heads. All they have to do is think “10 x 27 is 270… and then I just have to add another 27 to get 297. DONE!”
It’s so much easier to do the harder problems when you really understand the basics. Most people never understand the basics. They think they do. But they don’t.
Okay.
Back to the quiz.
The teacher obviously knows (I’m assuming) that 5 + 5 + 5 is the same as 3 + 3 + 3 + 3 + 3.
So why would one method be preferred over the other?
Because thinking of 5 x 3 as, literally, “five groups of three” will help them when they learn how to divide. (That’s what the Common Core standard here is getting at.)
When they see a problem that says 5 x ___ = 15, they’ll be thinking “I need five groups of SOME NUMBER to get to 15.” In other words, they’ll be able to pick up division a little more quickly because they’re learning the proper way to think now.
I don’t know if that’s exactly what the teacher was doing, but it’s plausible.
What about the array problem? This one’s even more straightforward.
It actually matters which way you draw the picture. But it’s not something kids will understand until they start using matrices in algebra class.
Even if you’re unfamiliar with matrices, here’s what you need to know: There’s a difference between a 2 x 3 matrix and a 3 x 2 matrix.
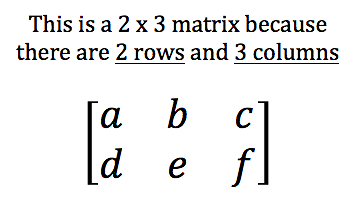
If you don’t draw it the right way, you’re not going to get those problems right.
I have taught kids matrices before. The ones who struggled would often confuse the order in which they put the numbers. So it helps to instill that idea at an early age.
So going back to the problem on this kid’s exam, it says to draw a 4 x 6 array. Even though it doesn’t matter right now, it will later make sense when they have to draw a matrix of 4 rows and 6 columns.
Teachers can’t always write these explanations down, so I understand why a kid’s parents would be confused when they see this exam. But there really is a method behind the madness. It’s not as arbitrary as you think, and there’s reason to believe this teacher knows exactly what he or she is doing.
If you’re looking at the exam and thinking “The kid got the right answers and that’s all that matters,” well… that’s why you’re not a teacher. I was in front of a classroom for several years and I know it’s entirely possible for a student to get the right answer without solving the problem correctly. Sometimes, that’s because of dumb luck. Sometimes, like in this case, the student just didn’t understand what the teacher was looking for.
I’m not saying I would have taken a full point off each of those questions, but the teacher wasn’t wrong to correct the student. The points didn’t come off because the answer was wrong. The points came off because the process the student was using won’t be helpful in the future.
Correcting that process right now, before the same student stumbles a few years later when the stakes are higher, makes a lot of sense to me. I think that’s all the teacher was trying to do.
Sometimes, getting the solution right isn’t all that matters.


It’s Moving Day for the Friendly ..."
It’s Moving Day for the Friendly ..."
It’s Moving Day for the Friendly ..."
It’s Moving Day for the Friendly ..."